【7.0】利用 AdaBoost 元算法提高分类性能
前言
当做重要决定时,大家可能都会考虑吸取多个专家而不只是一个人的意见。机器学习处理问题时也是如此,这就是元算法(meta—algorithm)背后的思路。元算法是对其他算法进行组合的一种方式。接下来我们将集中关注一个称作 AdaBoost(读作[ˈeɪdəˌbust]) 的最流行的元算法。
本文内容学习来源感谢:
- 《Machine Learning in Action》
- 《智能之门》
- 哔哩哔哩,维基百科等网络
前排说明
- 本文所有代码基于 Python 3.10 版本,理论上你的版本为 3.X 皆可运行。
- 在代码的注释中看到符号:❓,则表示注释的代码部分函数解释说明可以在0最后的相关函数中查阅。
基于数据集多重抽样的分类器
前面已经介绍了五种不同的分类算法,它们各有优缺点。我们自然可以将不同的分类器组合起来,而这种组合结果则被称为集成方法(ensemble method)或者元算法(meta-algorithm)。使 用集成方法时会有多种形式:可以是不同算法的集成,也可以是同一算法在不同设置下的集成,还可以是数据集不同部分分配给不同分类器之后的集成。
AdaBoost
- 优点:泛化错误率低,易编码,可以应用在大部分分类器上,无参数调整。
- 缺点:对离群点敏感。
- 适用数据类型:数值型和标称型数据。
bagging
Bagging(读作[ˈbæɡɪŋ]),它是 Bootstrap Aggregating (引导聚集算法,又称装袋算法)的缩写,是在从原始数据集选择 S 次后得到 S 个新数据集的一种技术。新数据集和原数据集的大小相等。每个数据集都是通过在原始数据集中随机选择一个样本来进行替换而得到的。这里的替换就意味着可以多次地选择同一样本。这一性质就允许新数据集中可以有重复的值,而原始数据集的某些值在新集合中则不再出现。
在S个数据集建好之后,将某个学习算法分别作用于每个数据集就得到了S个分类器。当我们要对新数据进行分类时,就可以应用这S个分类器进行分类。与此同时,选择分类器投票结果中最多的类别作为最后的分类结果。
Bagging在降低模型的方差和提高泛化能力方面表现出色,特别是在复杂模型和高维数据上。常见的Bagging算法包括随机森林(Random Forests),它是基于决策树的一种集成学习方法。
boosting
Boosting(提升方法)是一种与bagging很类似的技术。不论是在boosting还是bagging当中,所使用的多个分类器的类型都是一致的。但是在前者当中,不同的分类器是通过串行训练而获得的,每个新分类器都根据已训练出的分类器的性能来进行训练(通过串行训练多个弱学习器1(weak learners),然后将它们组合成一个强学习器(strong learner))。
Boosting 的核心思想是重点关注被前一轮弱学习器分类错误的样本,对它们进行加权,然后在下一轮中训练新的弱学习器来纠正之前的错误。由于boosting分类的结果是基于所有分类器的加权求和结果的,因此 boosting 与 bagging 不太一样。bagging中的分类器权重是相等的,而 boosting 中的分类器权重并不相等,每个权重代表的是其对应分类器在上一轮迭代中的成功度。
boosting 方法拥有多个版本,本章将只关注其中一个最流行的版本 AdaBoost。
训练算法:基于错误提升分类器的性能
能否使用弱分类器和多个实例来构建一个强分类器?这是一个非常有趣的理论问题。这里的“弱”意味着分类器的性能比随机猜测要略好,但是也不会好太多。这就是说,在二分类情况下弱分类器的错误率会高于 50%,而“强”分类器的错误率将会低很多。AdaBoost 算法即脱胎于上述理论问题。
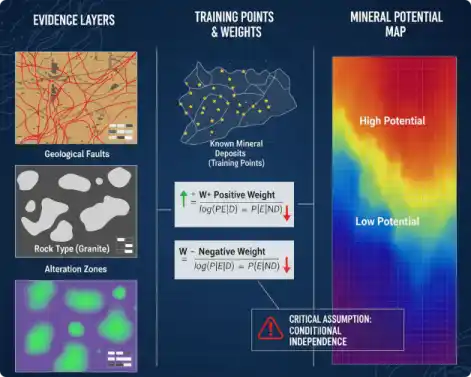
AdaBoost 运行过程如下:训练数据中的每个样本,并赋予其一个权重,这些权重构成了向量D。一开始,这些权重都初始化成相等值。首先在训练数据上训练出一个弱分类器并计算该分类器的错误率,然后在同一数据集上再次训练弱分类器。在分类器的第二次训练当中,将会重新调整每个样本的权重,其中第一次分对的样本的权重将会降低,而第一次分错的样本的权重将会提高。为了从所有弱分类器中得到最终的分类结果,AdaBoost 为每个分类器都分配了一个权重值 alpha ,这些 alpha 值是基于每个弱分类器的错误率进行计算的。其中,错误率 ε 的定义为:$\huge\varepsilon=\frac{未正确分类的样本数目}{所有样本数目}$ 。
而 alpha 的计算公式为:$\huge \alpha = \frac{1}{2} \ln{(\frac{1-\varepsilon}{\varepsilon})}$ 。其算法流程如下图所示:

计算出 alpha 值之后,可以对权重向量D进行更新,以使得那些正确分类的样本的权重降低而错分样本的权重升高。D的计算方法如下。
- 如果某个样本被正确分类,那么该样本的权重更改为:$\huge D_i^{(t+1)}=\frac{D_i^{(t)}e^{- \alpha}}{Sum(D)}$ 。
- 而如果某个样本被错分,那么该样本的权重更改为:$\huge D_i^{(t+1)}=\frac{D_i^{(t)}e^{ \alpha}}{Sum(D)}$ 。
在计算出D之后,AdaBoost又开始进入下一轮迭代。AdaBoost算法会不断地重复训练和调整权重的过程,直到训练错误率为 0 或者弱分类器的数目达到用户的指定值为止。
基于单层决策树构建弱分类器
单层决策树(decision stump,也称决策树桩)是一种简单的决策树。前面我们已经介绍了决策树的工作原理,接下来将构建一个单层决策树,而它仅基于单个特征来做决策。由于这棵树只有一次分裂过程,因此它实际上就是一个树桩。
现在我们创建一个名称为 adaboost.py 的新文件来添加如下代码:
1 | from numpy import * |
下图给出了上述数据集的示意图。如果想要试着从某个坐标轴上选择一个值(即选择一条与坐标轴平行的直线2)来将所有的圆形点和方形点分开,这显然是不可能的。这就是单层决策树难以处理的一个著名的问题。通过使用多棵单层决策树,我们就可以构建出一个能够对该数据集完全正确分类的分类器。

有了数据,接下来就可以通过构建多个函数来建立单层决策树。
第一个函数将用于测试是否有某个值小于或者大于我们正在测试的阈值。第二个函数则更加复杂一些,它会在一个加权数据集中循环,并找到具有最低错误率的单层决策树。现在在 adaboost.py 文件中添加如下代码:
1 | # 数据划分 |
现在我们使用如下代码进行测试:
1 | # 默认权重 0.2 |
运行结果如下所示:
1 | 划分信息: 当前划分特征 0, 划分阈值 0.9, 划分规则: lt, 错误权重 [[0.4]] |
上述单层决策树的生成函数是决策树的一个简化版本。它就是所谓的弱学习器,即弱分类算法。到现在为止,我们已经构建了单层决策树,并生成了程序,做好了过渡到完整 AdaBoost 算法的准备。
完整 AdaBoost 算法的实现
现在我们拥有了实现一个完整AdaBoost算法所需要的所有信息。AdaBoost 算法实现的伪代码如下所示:
1 | 对每次迭代: |
现在,在 adaboost.py 文件中添加如下代码:
1 | # AdaBoost 算法实现 |
函数名称尾部的DS代表的就是单层决策树(decision stump),它是AdaBoost中最流行的弱分类器,当然并非唯一可用的弱分类器。上述函数确实是建立于单层决策树之上的,但是我们也可以很容易对此进行修改以引入其他基分类器。
测试算法:基于AdaBoost的分类
一旦拥有了多个弱分类器以及其对应的alpha值,进行测试就变得相当容易了。在上面的adaBoostTrainDS()中,我们实际已经写完了大部分的代码。现在,需要做的就只是将弱分类器的训练过程从程序中抽出来,然后应用到某个具体的实例上去。每个弱分类器的结果以其对应的alpha值作为权重。所有这些弱分类器的结果加权求和就得到了最后的结果。
现在将如下代码添加到 adaboost.py 文件中:
1 | def adaClassify(datToClass,classifierArr): |
我尝试运行这段代码,它在 3.X 版本报错,如你所见,《Machine Learning in Action》 是在 2.x版本上实现的,我尝试修改了一些代码,例如alpha = float(0.5*log((1.0-error)/maximum(float(error),minFloat)))。但是它只能解决一小部分报错,它会带来其他报错,我有点困,不想动脑子,就暂时不修改它了,如果你感兴趣,自行尝试吧。
相关函数
inf
在NumPy中,**inf表示正无穷大(positive infinity)。它是一个特殊的浮点数常量,用于表示大于所有有限浮点数的值**。
-inf则表示负无穷大(negative infinity),表示小于所有有限浮点数的值。
这两个特殊值可以用于执行各种数学运算,例如除以零、计算极限等情况。当进行数值运算时,如果结果超过浮点数表示的范围,就会得到inf或-inf。
errArr[predictedVals == labelMat] = 0
errArr[predictedVals == labelMat] = 0 这个代码就有点抽象了,不过我们来一点点看,首先需要了解 predictedVals 和 labelMat 都是行数相同的矩阵(1 列),使用predictedVals == labelMat 会得到 true 或者 false 的结果,注意此结果是一个矩阵,然后根据结果矩阵的 true 来给对应的位置赋值 0。
如果你认为不理解,可以查看 NumPy 的文档 Boolean array indexing(布尔数组索引)
max()
在代码中的体现是 alpha = float(0.5*log((1.0-error)/max(error,1e-16)))。具体来说,max(error, 1e-16) 的作用是比较 error 和 1e-16 这两个数的大小,然后返回其中较大的那个数。如果 error 大于等于 1e-16,则返回 error,否则返回 1e-16。
1e-16 表示科学计数法中的小数,即 1 乘以 10 的负 16 次方,也就是 0.0000000000000001,它通常用于避免出现非常小的数值。这种写法在很多情况下用于处理误差或防止除零错误。通过将误差或某个数值与一个较小的阈值(如 1e-16)进行比较,可以确保得到一个非零的结果,避免出现异常或无效计算。
multiply()
multiply() 是 NumPy 库中的一个函数,用于对两个数组中对应位置的元素进行逐元素相乘。代码示例:
1 | import numpy as np |
sign()
sign() 是 NumPy 库中的一个函数,用于对数组中的元素进行符号函数运算,返回每个元素的正负号。代码示例:
1 | import numpy as np |
End
大概理解起来容易,但是实现起来又十分的繁杂且混乱😥